May — August 2024

Over the summer of 2024 I developed a program to generate a zoom of the Mandelbrot set in parallel using the Open Message Passing Interface (Open MPI) and the GNU Multiple Precision Floating-Point Reliable Library (GNU MPFR). I used the sender/receiver communication model to distribute frames to each process. As MPI doesn't support sending MPFR types, the bytes are manually dumped into a buffer and reconstructed on the reciving end. This was my first project using MPI, and it is really fun and challenging to develop. It makes some beautiful videos and it is amazing how fast it is. The media to the left was created using Texas A&M's high performance computing resources.

January — April 2024

Over the spring semester of 2024, I participated in the directed reading program in the mathematics department at Texas A&M University. I read Sipser's book titled "Introduction to the Theory of Computation." My mentor was Ben Warren. Our product for the semester was to give a presentation on a subject in our book that interested us. I gave an introductory talk on undecidability and Turing machines, linked to the left. Overall it was a great experience, and I highly recommend it.

January 2023

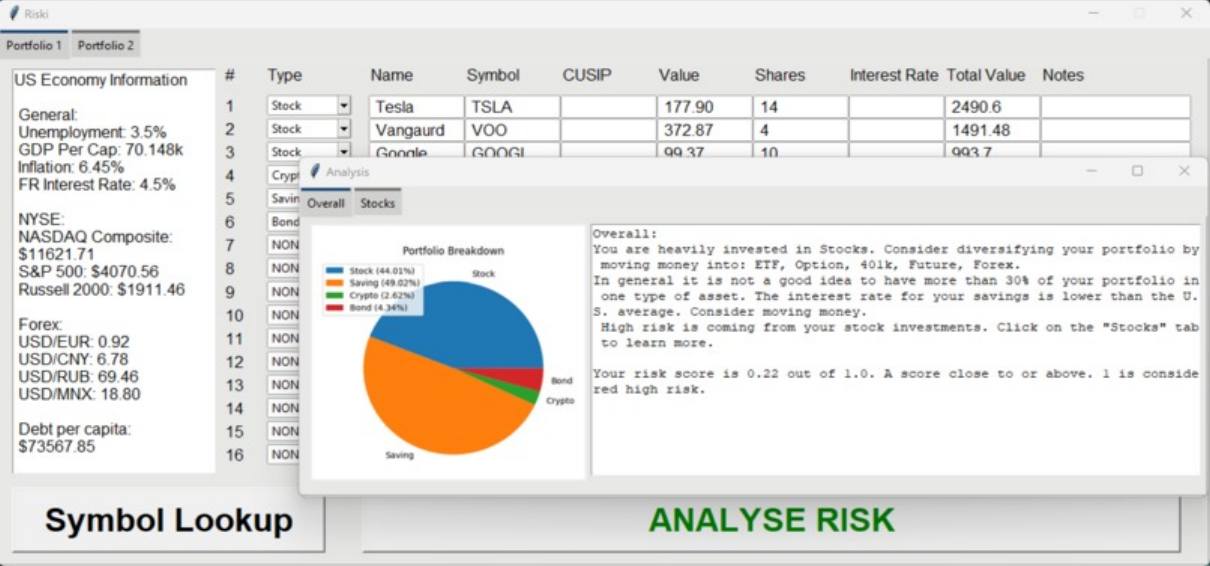
Riski was the product of a 24-hour hackathon called "TAMUhack" at Texas A&M created by myself, that won Goldman Sach's risk analysis challenge. It was an application that uses Yahoo finances' API along with other APIs to calculate the risk of a given portfolio. It also used the U.S. Bureau of Labor Statistics API. The code can be found here and the official devpost can be found here.

October 2022

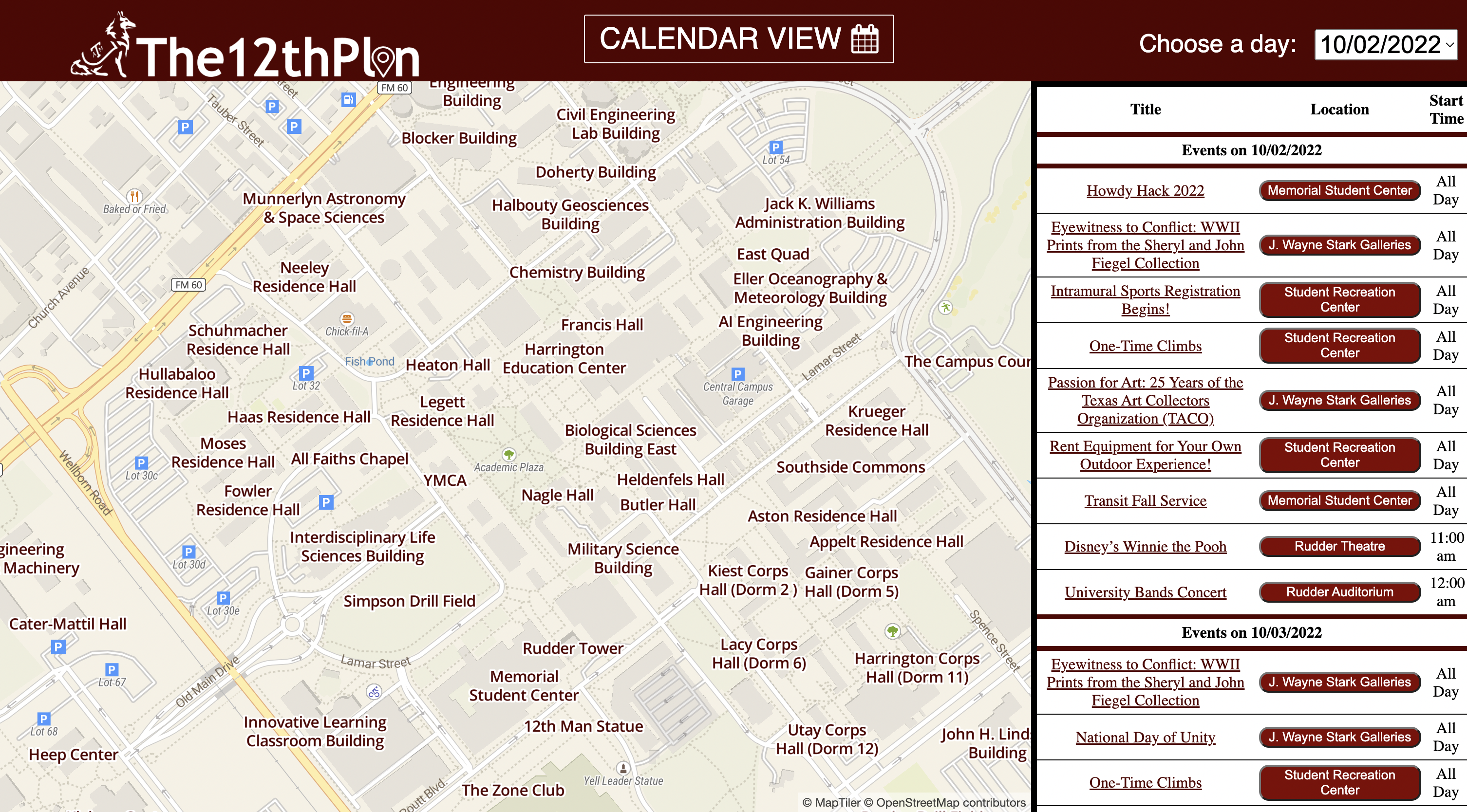
The12thPlan was the product of a 24-hour hackathon called "HowdyHack" at Texas A&M created by Alline Ayala, Avery Reagan, and myself that won us the "Best Aggie Hack". It was a web application that rips calendar and map data from Texas A&M's website and then displays it in a user-friendly manner. We also had a feature where you could click on the location of the event, and you would fly there on the map. We used so many tools including: HTML, CSS, JavaScript, Python, JSON, and even googles location API. The code can be found here and the official devpost can be found here.

June 2022

Wave function collapse takes the idea of the wave function, a mathematical representation of the state of a quantum system, and applies it to the generation of 2D tile-based maps. In this project, a wave is taken in and analyzed. Then the rules of the input wave, shown to the left, are used to generate a new wave, shown to the right. This project was heavily inspired by the work of Maxim Gumin.

May — June 2022

Strange Attractors are a chaotic set of 3D parametric differential equations that describe an oscillating system. They were discovered while using the Navier-Stokes equation to study oscillating fluid systems such as chemical reactions and weather patterns. I decided to research them, and this project was produced from it. The main product of this project can be found here, a website where you can change the attributes that describe these beautiful systems and interact with them. Since they are 3D, you can also spin them around and zoom in and out. I first learned about these systems a while ago from a coding train video and my other sources to find and understand these strange attractors are found on the remote repository here.

October 2022

The Lyapunov fractal is a fractal that is created by the Lyapunov exponent of a system. The Lyapunov exponent is a measure of the rate of divergence of a system; more about it can be found here. This is a very interesting fractal because a measure of chaos creates it. The image shown along with the images found on the GitHub repo are all created utilizing Texas A&M's HPRC resources. I was inspired to create this fractal by a YouTube video by Desdenova seen here.

February 2022

Chrome Crack is a collection of scripts that, when put together, allow the passwords saved by Google to be cracked and exported to a "flash drive". This process only required one simple step: the flash drive to be plugged in. The flash drive used is the RubberDucky by Hak5, and is not actually a flash drive. The program is broken up into two parts. The first is to inject a script that runs keystrokes on the target computer via the RubberDucky. The second is the Python file "ChromeCrack.py," downloaded onto the target computer. The process of cracking the encrypted file Google stores passwords on must be done on the target computer as it uses the OS' encryption key. Once "ChromeCrack.py" is run, the passwords are saved to the RubberDucky. An episode of Mr. Robot inspired this project.

January 2022

Newton's method is a recursive algorithm that uses the derivative of a function to approximate its roots. On holomorphic functions, fractals are created by the convergence and divergence of this method. The example shown is using the function $z^3 - 1$ with roots $-\frac{1}{2} \pm \frac{\sqrt{3}}{2}i$ and $1$. Each color in the image represents which root Newton's method converges to. When creating this, I learned about the complex plane, how to work with complex numbers, and re-discovered Euler's formula.